Dot Product Tricks
When I first started 3D programming and came across the dot product, I was confused about it. I couldn’t wrap my head around how it could be used.
Here are some neat use cases I found throughout the years for it
It tells you how similar two normalized vectors are #
The dot product returns a value in the range of [-1, +1].
+1 means the vectors are 100% the same
0 means that the vectors are perpendicular/orthogonal to each other
-1 means the vectors are pointing 100% in the opposite direction
float similarity = DotProduct(vec_a, vec_b);
Vector Projection #
Remove a vector from another #
In this example we cancel out the velocity in “gravity direction”.
// cancel out gravity part from velocity
const Vec3 vel = state.velocity - state.gravityNormal * DotProduct( state.velocity, state.gravityNormal );
This gives you the length of velocity in the gravity direction
DotProduct( state.velocity, state.gravityNormal )
Angle between two normalized vectors #
This is useful when you want to get the angle between two vectors. float angle_rad = acosf(DotProduct(normalized_vec_a, normalized_vec_b));
Note that the range of angle will be 0° ≤ angle ≤ 180 degrees and the equivalent in radians 0° ≤ angle ≤ PI radians
The acos gives you only the magnitude of the angle between the vectors, it doesn’t give you the direction.
If you use this to rotate an object using this angle, you’ll need to make adjustment to the result if you want to make it look at a target for example.
// Define a normal (usually something like vec3(0, 0, 1) for XY plane)
vec3 normal = ...;
float angle = acos(DotProduct(normalized_a, normalized_b)); // 0 to π
vec3 cross = CrossProduct(normalized_a, normalized_b);
// Use the direction of the cross product to determine sign
if (DotProduct(cross, normal) < 0) {
angle = 2 * M_PI - angle;
}
Clip vector to plane #
I’m not sure what the proper terminology is to describe this, but you can use the dot product in the following way to change the length of vectorToClip so that it ends up on the plane normal.
Vec3 VectorClipToVectorPlane( const Vec3 &planeNormal, const Vec3 &vectorToClip ) {
return vectorToClip / DotProduct( planeNormal, vectorToClip );
}
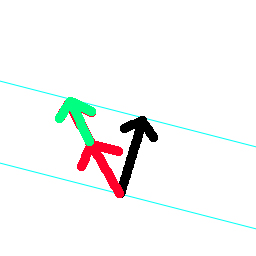
This clips the red vector to the plane of the black vector.
Visibility tests #
Back face culling #
If you want to check, you are viewing the front side of a triangle, you can use this. This can be used for checking, if something is looking at something
float backface_culled = DotProduct( plane_normal, view_dir );
if (backface_culled < 0)
{
// not visible
}
float is_looking_at = DotProduct( enemy_view_dir, VectorNormalize( other_obj_pos - enemy_pos ) );
if (is_looking_at >= 0)
{
// sees the front face of the other object
}
View Cone Visibility #
You can expand the above case to a view cone of a specified angle width
float is_looking_at = DotProduct( enemy_view_dir, VectorNormalize( other_obj_pos - enemy_pos ) );
const float DEGREES_TO_RADIANS = static_cast < float >( M_PI ) / 180.0f;
float dot_angles = cosf( 45.0f * DEGREES_TO_RADIANS );
if (is_looking_at >= dot_angles )
{
// other object is in view cone of enemy
}